When modeling dataset we often need to represent hierarchical relation between objects. If the information is easy to store in a classical RDBMS querying the full hierarchical structure might not be obvious at the first glance. In this article we show it by illustrating a simple but common example, building a Table of Content (which is inherently a tree) out from sections that only point towards their parents.
Understanding recursion implementation
Recursion is implemented in SQL as the UNION of two CTE (common table expressions). The first CTE is the initial condition, it seeds the process and defines the interface: table name and column types. The second CTE is the recursion loop which is responsible for the computations and the halting condition (recursive query may loop forever).
Simple counter
The query below implements a simple countdown process:
- It defines the interface as a table named countdown with a single integral column named counter;
- Then it withdraw one unit at each recursion step while the previous step counter is greater than zero.
WITH RECURSIVE countdown(counter) AS (
(
-- Initial condition:
SELECT 5::INTEGER AS counter
)
-- Concatenation of steps:
UNION ALL
-- Current recursion step:
SELECT C.counter - 1 AS counter -- Some recursion computations
FROM countdown AS C -- Based on previous recursion step
WHERE C.counter > 0 -- With an halting condition (previous step)
)
-- Actually execute the recursion:
SELECT * FROM countdown;As expected, it counts down from five to zero. And indeed as the CTE are plain standard SQL the final select may use the full power of SQL instructions. Instead of simply select we can aggregate as we wish:
SELECT SUM(counter) FROM countdown; -- 15That is, we implemented a totally inefficient way to compute triangular numbers to show a very basic usage of recursion.
Trendy recursion problem
Before diving in tree building example, let’s implement a real world recursion example with a bit more content than the simple counter. We pick the Collatz Conjecture which is a very trendy recursion nowadays. We could summarize the problem statement as follow:
WITH RECURSIVE collatz(altitude) AS (
(
-- Initial condition:
SELECT 15::INTEGER AS altitude
)
-- Concatenation of results:
UNION ALL
-- Recursion:
SELECT
CASE WHEN C.altitude % 2 = 0 -- Check parity
THEN C.altitude/2 -- Even case
ELSE C.altitude*3 + 1 -- Odd case
END AS altitude
FROM collatz AS C -- Based on previous step
WHERE C.altitude > 1 -- Stop when flight has landed
)
-- Execute:
SELECT array_agg(altitude) FROM collatz; -- {15,46,23,70,35,106,53,160,80,40,20,10,5,16,8,4,2,1}
SELECT COUNT(*) FROM collatz; -- 18Results are compliant with the Collatz series definition, it flights as expected during 18 steps. This method can be extended to any integral number using FUNCTION, but this is out of the scope of this article.
The point to grasp is recursive query allows us to implicitly write a while loop as a recursive table. This is very handing because a lot of smart data structure such as graph and well known mathematical operations can be parsed or defined by recursion. That’s why recursive queries are so useful.
Random walk
Recursive query can also be used to perform random walk operations, and it nicely fits with PostGIS extension. Let’s say we want to generate a random walk confined within the Brussels’ Centrum, that is a job for recursive query.
WITH RECURSIVE randomwalk(id, location) AS (
(
-- Initial condition:
SELECT
0::INTEGER AS id,
ST_Transform(
ST_SetSRID( -- Let's pretend we are in Brussels...
ST_MakePoint(4.3517103, 50.8503396), 4326
), 31370
) AS location, -- ...in an almost flat geometry using a Lambert projection
ST_Transform( -- And we want to stay inside the centrum
ST_GeomFromText('POLYGON((4.33786236816723 50.84921725514839,4.342861238711385 50.83396766998021,4.348141735765069 50.832989392387454,4.365672985983299 50.84063719797648,4.369052504097658 50.84739468070037,4.367573964922627 50.852373252232184,4.346663196590037 50.85850683288841,4.33786236816723 50.84921725514839))', 4326), 31370
) AS limit_area
)
-- Concatenation of steps:
UNION ALL
-- Current recursion step:
SELECT
RW.id + 1 AS id,
ST_GeometryN(
ST_GeneratePoints( -- Randomly sample around current location
ST_Buffer(RW.location, 100), 1 -- Within a circle of radius of 100m
), 1
) AS location,
RW.limit_area
FROM randomwalk AS RW -- Based on previous recursion step
WHERE ST_Intersects(RW.location, RW.limit_area) -- While we stay within the centrum
)
-- Actually execute the recursion:
SELECT
id,
ST_Transform(location, 4326) AS location,
ST_MakeLine(
ST_Transform(location, 4326),
ST_Transform(LEAD(location) OVER (), 4326)
) AS edge
FROM randomwalk;Using the above procedure to sample and store five draws, it renders as follow:
Spanning a whole tree using recursion
Time to address our challenge, we want to build a Table of Content based on sections pointing towards their parent section.
Creating the trial dataset
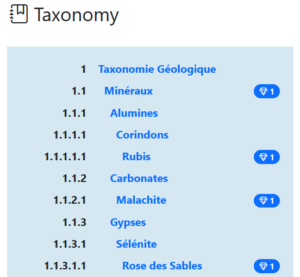
First we create a trial dataset to shoulder the discussion. Here we are using a subset of a geological taxonomy (sections come from my daughter’s gem collection) where each section of the Table of Content is a specific geological taxon.
CREATE TABLE IF NOT EXISTS section(
id UUID NOT NULL,
parent_id UUID,
key VARCHAR(128) NOT NULL,
CONSTRAINT section_pkey PRIMARY KEY (id),
CONSTRAINT section_key_uq UNIQUE (key),
CONSTRAINT section_parent_id_fk FOREIGN KEY(parent_id) REFERENCES section(id)
);
INSERT INTO section(id, parent_id, key) VALUES
('eb0d6bdf-7a50-4790-89b7-24dde230f5ca', NULL, 'Taxonomie Géologique'),
('ebe371af-7db6-40c8-8dc4-19768262cd20', 'eb0d6bdf-7a50-4790-89b7-24dde230f5ca', 'Minéraux'),
('37c82380-d149-4445-9652-c7bf71f72454', 'ebe371af-7db6-40c8-8dc4-19768262cd20', 'Alumines'),
('33fdfcbb-167d-40ee-b91c-b4e44bf964d2', '37c82380-d149-4445-9652-c7bf71f72454', 'Corindons'),
('0721c7e9-5c13-43de-bd80-330cfdc57147', '33fdfcbb-167d-40ee-b91c-b4e44bf964d2', 'Rubis'),
('d1a1f60b-5406-48a7-a62b-97df7fef9023', 'ebe371af-7db6-40c8-8dc4-19768262cd20', 'Carbonates'),
('a6adc748-ca54-4c6e-937d-245b2f872f01', 'd1a1f60b-5406-48a7-a62b-97df7fef9023', 'Malachite'),
('961efcb0-8dc2-4d82-9ddb-83f67d0a3357', 'ebe371af-7db6-40c8-8dc4-19768262cd20', 'Cyclooctasoufre'),
('c2720430-3964-4798-b298-03951500fbd1', 'ebe371af-7db6-40c8-8dc4-19768262cd20', 'Gypses'),
('9f868de6-6859-48c8-a05c-816d2e396828', 'c2720430-3964-4798-b298-03951500fbd1', 'Sélénite'),
('c8801884-cb96-4487-9799-4a461f5f1128', '9f868de6-6859-48c8-a05c-816d2e396828', 'Rose des Sables'),
('fc52ea4d-bb52-4f11-9656-1a3c02f8ead6', 'ebe371af-7db6-40c8-8dc4-19768262cd20', 'Pyrite'),
('e68f47b8-f05d-4e19-8c79-3fa43c2addf7', 'ebe371af-7db6-40c8-8dc4-19768262cd20', 'Silicates'),
('1d70d9a5-2920-43bd-bfaf-0a28513b3745', 'e68f47b8-f05d-4e19-8c79-3fa43c2addf7', 'Cyclosilicates'),
('631db215-e7c4-4946-9407-8154e741eacf', '1d70d9a5-2920-43bd-bfaf-0a28513b3745', 'Emeraude'),
('61a96742-19b8-4f98-9d46-96f465eb95a4', 'e68f47b8-f05d-4e19-8c79-3fa43c2addf7', 'Inosilicates'),
('9f7f03b2-417d-4214-bbdd-8876ae6188ab', '61a96742-19b8-4f98-9d46-96f465eb95a4', 'Jades'),
('41709fd4-ebd3-496c-a06b-a71638c6898e', '9f7f03b2-417d-4214-bbdd-8876ae6188ab', 'Jadéite'),
('a21e133c-96be-4a80-8e47-491ec6f61de7', 'e68f47b8-f05d-4e19-8c79-3fa43c2addf7', 'Nésosubsilicates'),
('08d09a47-c716-48d2-8a24-7e7808f5c2e7', 'a21e133c-96be-4a80-8e47-491ec6f61de7', 'Topaze'),
('fcecfb2c-bc2b-4c42-9fd8-7d6eeac8f834', 'e68f47b8-f05d-4e19-8c79-3fa43c2addf7', 'Tectosilicates'),
('041dd656-f43f-4eb5-9d94-3316a05c9dac', 'fcecfb2c-bc2b-4c42-9fd8-7d6eeac8f834', 'Feldspaths'),
('cbff09db-0689-42af-bf1c-c8f6420c8642', 'fcecfb2c-bc2b-4c42-9fd8-7d6eeac8f834', 'Quartz'),
('9ebbd265-154d-4839-b2a0-30eef22d0041', 'cbff09db-0689-42af-bf1c-c8f6420c8642', 'Améthyste'),
('a43c3309-72e3-446f-9468-d1ca90491f75', 'cbff09db-0689-42af-bf1c-c8f6420c8642', 'Aventurine'),
('c6d59c64-227e-4a26-a0f4-423b5d3b5cab', 'cbff09db-0689-42af-bf1c-c8f6420c8642', 'Calcédoines'),
('2abb66a5-587f-496a-bcba-07cad80f11c9', 'c6d59c64-227e-4a26-a0f4-423b5d3b5cab', 'Agate'),
('40d26aa9-1bab-48bc-89cc-641943464adc', 'c6d59c64-227e-4a26-a0f4-423b5d3b5cab', 'Jaspe'),
('157d14da-6308-4b25-9691-70aea27bdaf4', 'cbff09db-0689-42af-bf1c-c8f6420c8642', 'Oeil de Tigre'),
('c15059b9-ea11-43c6-a044-0f1a281696e2', 'fcecfb2c-bc2b-4c42-9fd8-7d6eeac8f834', 'Sodalite'),
('d078430f-6819-417d-ac6f-33ec73d6cda8', 'eb0d6bdf-7a50-4790-89b7-24dde230f5ca', 'Roches'),
('adad0a95-93f5-4e51-affd-c66a018c1a81', 'd078430f-6819-417d-ac6f-33ec73d6cda8', 'Roches métamorphiques'),
('586f1635-f300-4be8-96a3-979ec398e886', 'd078430f-6819-417d-ac6f-33ec73d6cda8', 'Roches sédimentaires'),
('59ec3d9e-7851-484b-a1b7-dace05083af9', '586f1635-f300-4be8-96a3-979ec398e886', 'Fossiles'),
('be26a3a1-f143-4dcc-a34f-c4e7a0e9a504', '59ec3d9e-7851-484b-a1b7-dace05083af9', 'Ambre'),
('bd77937e-be91-4db5-b784-c76a78f864ad', '59ec3d9e-7851-484b-a1b7-dace05083af9', 'Ichnofossiles'),
('b730a514-4a6d-4fa8-894b-e42dc26a1aa0', '59ec3d9e-7851-484b-a1b7-dace05083af9', 'Microfossile'),
('2b3b06cd-88a8-4c25-87dc-252af93d9e27', '59ec3d9e-7851-484b-a1b7-dace05083af9', 'Stromatolithe'),
('3e34f107-8011-4a88-891b-708875e8c3d6', 'd078430f-6819-417d-ac6f-33ec73d6cda8', 'Roches volcaniques'),
('7ed71355-748e-448c-acae-87eada183796', '3e34f107-8011-4a88-891b-708875e8c3d6', 'Obsidiène');In this example, the tree structure is encoded as an edge list where each node points towards its own parent. If no cycle are present this data model is a tree.
Implementing recursive query
Recall a recursive query is made of as the union of two queries:
- Initial condition will seed the result set with root nodes (nodes with no parent are top section titles);
- Recursive steps which will follow parent edges and recursively seeds sub-sections tree level by tree level.
Additionally the query must stop, meaning at some point recursion query must return no rows and make the recursion ends. In this specific case the recursion will stop when all sibling sections are reached and it will take exactly n + 1 steps where n is the tree depth. Notice, the halting condition is held in the data structure itself and their properties are extensively studied, here it is a special case of Depth First Search.
WITH RECURSIVE taxonomy(id, key, path, toc, bullet, depth) AS (
(
-- Init with root nodes:
SELECT
id,
key,
'{}'::TEXT[] AS path, -- Collect section titles in order
ARRAY[row_number() OVER ()] AS toc, -- Collect section order index
(row_number() OVER ())::TEXT AS bullet, -- Create the section bullet item
1 AS depth -- Tree depth
FROM collection_taxon
WHERE parent_id IS NULL
ORDER BY path
)
UNION ALL
-- Recursively collect all children nodes for each tree level:
SELECT
sub.id,
sub.key,
array_cat(t.path, ARRAY[sub.key]::TEXT[]),
array_cat(t.toc, ARRAY[row_number() OVER (PARTITION BY t.toc ORDER BY t.toc, sub.key)]),
t.bullet || '.' || row_number() OVER (PARTITION BY t.toc ORDER BY t.toc, sub.key),
t.depth + 1
FROM collection_taxon AS sub, taxonomy AS t -- Join current table to the previous state...
WHERE sub.parent_id = t.id -- ...and recurse by following parent edges
-- Hopefully it will end when all leaf nodes are reached
)
-- Add extra metadata to nodes:
SELECT
LEFT(C.parent_id::TEXT, 8) AS parent_id,
LEFT(C.id::TEXT, 8) AS id,
C.key,
T.path, T.toc, T.depth, T.bullet
FROM
collection_taxon AS C
JOIN taxonomy AS T USING(id)
ORDER BY toc, C.key;With our trial dataset, the final result looks like:
| parent_id | id | key | path | toc | depth | bullet |
| NULL | eb0d6bdf | Taxonomie Géologique | {} | {1} | 1 | 1 |
| eb0d6bdf | ebe371af | Minéraux | {Minéraux} | {1,1} | 2 | 1.1 |
| ebe371af | 37c82380 | Alumines | {Minéraux,Alumines} | {1,1,1} | 3 | 1.1.1 |
| 37c82380 | 33fdfcbb | Corindons | {Minéraux,Alumines,Corindons} | {1,1,1,1} | 4 | 1.1.1.1 |
| 33fdfcbb | 0721c7e9 | Rubis | {Minéraux,Alumines,Corindons,Rubis} | {1,1,1,1,1} | 5 | 1.1.1.1.1 |
| ebe371af | d1a1f60b | Carbonates | {Minéraux,Carbonates} | {1,1,2} | 3 | 1.1.2 |
| d1a1f60b | a6adc748 | Malachite | {Minéraux,Carbonates,Malachite} | {1,1,2,1} | 4 | 1.1.2.1 |
| ebe371af | 961efcb0 | Cyclooctasoufre | {Minéraux,Cyclooctasoufre} | {1,1,3} | 3 | 1.1.3 |
| ebe371af | c2720430 | Gypses | {Minéraux,Gypses} | {1,1,4} | 3 | 1.1.4 |
| c2720430 | 9f868de6 | Sélénite | {Minéraux,Gypses,Sélénite} | {1,1,4,1} | 4 | 1.1.4.1 |
| 9f868de6 | c8801884 | Rose des Sables | {Minéraux,Gypses,Sélénite,”Rose des Sables”} | {1,1,4,1,1} | 5 | 1.1.4.1.1 |
| ebe371af | fc52ea4d | Pyrite | {Minéraux,Pyrite} | {1,1,5} | 3 | 1.1.5 |
| ebe371af | e68f47b8 | Silicates | {Minéraux,Silicates} | {1,1,6} | 3 | 1.1.6 |
| e68f47b8 | 1d70d9a5 | Cyclosilicates | {Minéraux,Silicates,Cyclosilicates} | {1,1,6,1} | 4 | 1.1.6.1 |
| 1d70d9a5 | 631db215 | Emeraude | {Minéraux,Silicates,Cyclosilicates,Emeraude} | {1,1,6,1,1} | 5 | 1.1.6.1.1 |
| e68f47b8 | 61a96742 | Inosilicates | {Minéraux,Silicates,Inosilicates} | {1,1,6,2} | 4 | 1.1.6.2 |
| 61a96742 | 9f7f03b2 | Jades | {Minéraux,Silicates,Inosilicates,Jades} | {1,1,6,2,1} | 5 | 1.1.6.2.1 |
| 9f7f03b2 | 41709fd4 | Jadéite | {Minéraux,Silicates,Inosilicates,Jades,Jadéite} | {1,1,6,2,1,1} | 6 | 1.1.6.2.1.1 |
| e68f47b8 | a21e133c | Nésosubsilicates | {Minéraux,Silicates,Nésosubsilicates} | {1,1,6,3} | 4 | 1.1.6.3 |
| a21e133c | 08d09a47 | Topaze | {Minéraux,Silicates,Nésosubsilicates,Topaze} | {1,1,6,3,1} | 5 | 1.1.6.3.1 |
| e68f47b8 | fcecfb2c | Tectosilicates | {Minéraux,Silicates,Tectosilicates} | {1,1,6,4} | 4 | 1.1.6.4 |
| fcecfb2c | 041dd656 | Feldspaths | {Minéraux,Silicates,Tectosilicates,Feldspaths} | {1,1,6,4,1} | 5 | 1.1.6.4.1 |
| fcecfb2c | cbff09db | Quartz | {Minéraux,Silicates,Tectosilicates,Quartz} | {1,1,6,4,2} | 5 | 1.1.6.4.2 |
| cbff09db | 9ebbd265 | Améthyste | {Minéraux,Silicates,Tectosilicates,Quartz,Améthyste} | {1,1,6,4,2,1} | 6 | 1.1.6.4.2.1 |
| cbff09db | a43c3309 | Aventurine | {Minéraux,Silicates,Tectosilicates,Quartz,Aventurine} | {1,1,6,4,2,2} | 6 | 1.1.6.4.2.2 |
| cbff09db | c6d59c64 | Calcédoines | {Minéraux,Silicates,Tectosilicates,Quartz,Calcédoines} | {1,1,6,4,2,3} | 6 | 1.1.6.4.2.3 |
| c6d59c64 | 2abb66a5 | Agate | {Minéraux,Silicates,Tectosilicates,Quartz,Calcédoines,Agate} | {1,1,6,4,2,3,1} | 7 | 1.1.6.4.2.3.1 |
| c6d59c64 | 40d26aa9 | Jaspe | {Minéraux,Silicates,Tectosilicates,Quartz,Calcédoines,Jaspe} | {1,1,6,4,2,3,2} | 7 | 1.1.6.4.2.3.2 |
| cbff09db | 157d14da | Oeil de Tigre | {Minéraux,Silicates,Tectosilicates,Quartz,”Oeil de Tigre”} | {1,1,6,4,2,4} | 6 | 1.1.6.4.2.4 |
| fcecfb2c | c15059b9 | Sodalite | {Minéraux,Silicates,Tectosilicates,Sodalite} | {1,1,6,4,3} | 5 | 1.1.6.4.3 |
| eb0d6bdf | d078430f | Roches | {Roches} | {1,2} | 2 | 1.2 |
| d078430f | adad0a95 | Roches métamorphiques | {Roches,”Roches métamorphiques”} | {1,2,1} | 3 | 1.2.1 |
| d078430f | 586f1635 | Roches sédimentaires | {Roches,”Roches sédimentaires”} | {1,2,2} | 3 | 1.2.2 |
| 586f1635 | 59ec3d9e | Fossiles | {Roches,”Roches sédimentaires”,Fossiles} | {1,2,2,1} | 4 | 1.2.2.1 |
| 59ec3d9e | be26a3a1 | Ambre | {Roches,”Roches sédimentaires”,Fossiles,Ambre} | {1,2,2,1,1} | 5 | 1.2.2.1.1 |
| 59ec3d9e | bd77937e | Ichnofossiles | {Roches,”Roches sédimentaires”,Fossiles,Ichnofossiles} | {1,2,2,1,2} | 5 | 1.2.2.1.2 |
| 59ec3d9e | b730a514 | Microfossile | {Roches,”Roches sédimentaires”,Fossiles,Microfossile} | {1,2,2,1,3} | 5 | 1.2.2.1.3 |
| 59ec3d9e | 2b3b06cd | Stromatolithe | {Roches,”Roches sédimentaires”,Fossiles,Stromatolithe} | {1,2,2,1,4} | 5 | 1.2.2.1.4 |
| d078430f | 3e34f107 | Roches volcaniques | {Roches,”Roches volcaniques”} | {1,2,3} | 3 | 1.2.3 |
| 3e34f107 | 7ed71355 | Obsidiène | {Roches,”Roches volcaniques”,Obsidiène} | {1,2,3,1} | 4 | 1.2.3.1 |
And can be checked against a graph visualization software (section order is not taken into account here):
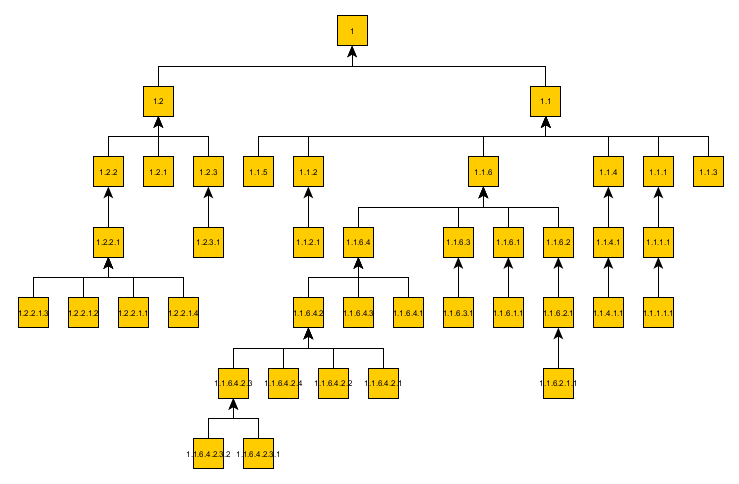
And voilà! We implemented a tree builder for a Table of Content based on a Geological Taxonomy. The resulting query can be then passed to another workflow such as a document rendering system to express the TOC with styles and links: