Bifurcation diagram

Sometimes, it is just fun to do some simple math and get nice figure, why not drawing some bifurcation diagrams.

How it works

To draw a bifurcation diagram, we need to find some recurrence relation that exhibits chaotic behaviour. A nice place to find them is to use Euler method for specific dynamic system such as logistic systems.

For this specific recurrence:

   

Where is our parameter and will be some initial condition, there are multiple different behaviour (we may want to discard some few first points) for the series: stability, multiple equilibrium points and chaos.

We can implement the recurrence function as follow:

def model(x, r):
    return r * x * (1. - x)

And we create a function that compute the first terms and may keep only the last terms:

def diagram(r, x=0.1, n=1200, m=200):
    if not isinstance(x, np.ndarray):
        x = np.full(r.size, x)
    xs = []
    for i in range(n):
        if i >= n - m:
            xs.append(x)
        x = model(x, r)
    return np.array(xs).T

Now we can compute the 30 first terms of the recurrence relation for several values of parameter to see what are the behaviour of the generated series:

rtest = np.array([0., 0.5, 1.5, 3.0, 3.1, 3.5, 4.0])
xtest = diagram(rtest, n=30, m=30)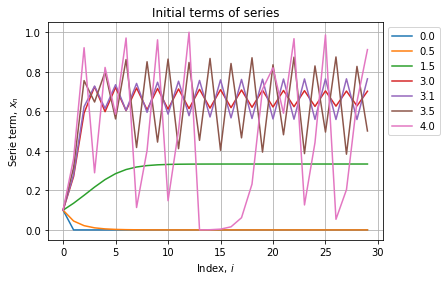

As expected all series starts at 0.1, some converges to a constant other oscillate between two or more specific values. We can see further to check if the behaviour stabilizes:

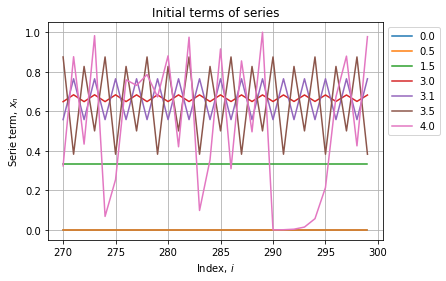
Now instead of plotting last series terms wrt to their index, we will assess them wrt the parameter . We also will test multiple values of initial conditions and assign them different colors.

rlin = np.linspace(-2, 4, 500)
xlin = np.linspace(-0.1, 0.1, 2)
clin = np.linspace(0., 1., xlin.size)
colors = plt.get_cmap("cool")(clin)

The bifurcation diagram will then we plotted as follow:

fig, axe = plt.subplots(figsize=(8, 6))
for x0, color in zip(xlin, colors):
    x = diagram(rlin, x=x0, n=600, m=100)
    axe.plot(rlin, x, ',', color=color)
axe.set_title("Bifurcation diagram")
axe.set_xlabel("Parameter, ")
axe.set_ylabel("Serie term, ")
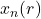axe.grid()

And renders as:

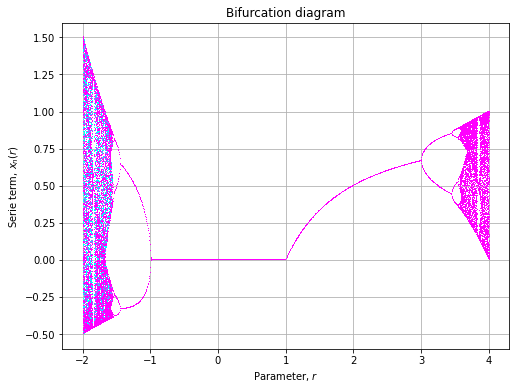
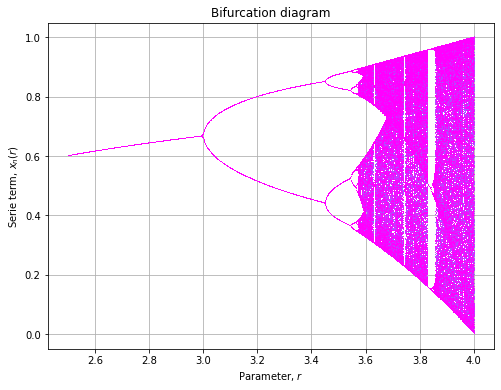
Examples

Lets plot more of them with this all on one plotting function:

def plot(model, rlin=None, xlin=None, colors=None, n=1200, m=200, rmin=-20, rmax=20, rsize=1000, cmap="cool", axe=None):
    
    if rlin is None:
        rlin = np.linspace(rmin, rmax, rsize)
    
    if xlin is None:
        xlin = np.linspace(-0.5, 0.5, 10)
    
    if colors is None:
        clin = np.linspace(0., 1., xlin.size)
        colors = plt.get_cmap(cmap)(clin)
    
    if axe is None:
        fig, axe = plt.subplots(figsize=(8, 6))
    
    for x0, color in zip(xlin, colors):
        x = diagram(model, rlin, x=x0, n=600, m=100)
        axe.plot(rlin, x, ',', color=color)
    
    axe.set_title("Bifurcation diagram")
    axe.set_xlabel("Parameter, ")
    axe.set_ylabel("Serie term, ")
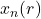    axe.grid()
    
    return axe

Biological system

   

def sigmoid(x, r):
    return 5.821 * np.tanh(1.487 * x) - r * np.tanh(0.2223 * x)

axe = plot(
    model=sigmoid,
    rmin=5, rmax=30,
    xlin=np.array([-0.1, 0.1])
)

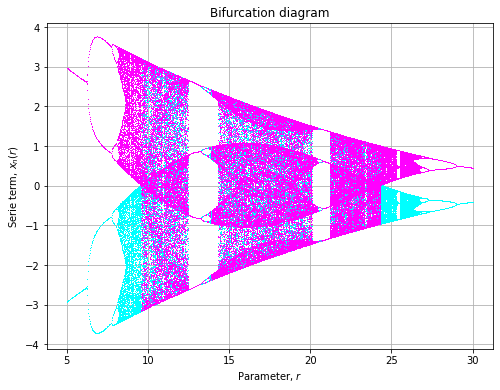
Sinusoidal

   

def sinusuodal(x, r, p=0.7):
    return r * x ** 2 * np.sin(np.pi * x) + p

axe = plot(
    model=sinusuodal,
    rmin=-2.7, rmax=1.4,
    xlin=np.array([-0.1, 0.1])
)

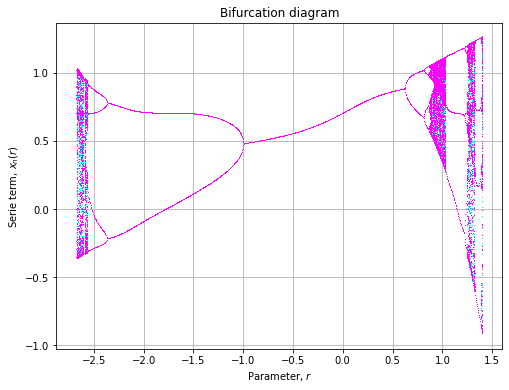
Cosinusoidal

   

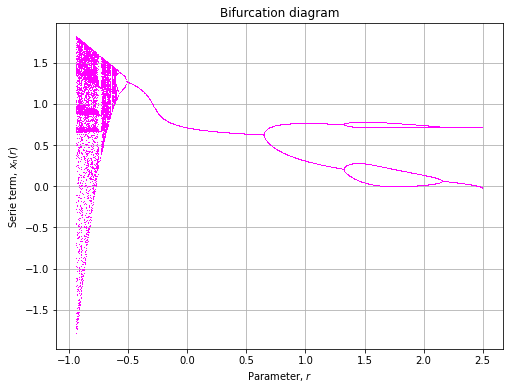
def cosinusuodal(x, r, p=0.7):
    return r * x ** 2 * np.cos(np.pi * x) + p

axe = plot(
    model=cosinusuodal,
    rmin=-1, rmax=2.5,
    xlin=np.array([-0.1, 0.1])
)