This post shows how to solve the Ballistic problem with Drag Force taken into account.
Setup
We import required libraries:
import numpy as np
import matplotlib.pyplot as plt
from scipy import integrateThe model can be expressed as follow:
![]()
Which can be projected:
![]()
And then linearized:
def model(t, x, m, g, c):
return np.array([
x[2],
x[3],
- c * x[2] / m,
- g - c * x[3] / m
])We also define two events function (root finding) for to trigger when Apex and Ground are found over the trajectory:
def apex(t, x, m, g, c):
return x[3]We monkey-patch the second function to interrupt the integration process when projectile hit the ground:
def ground(t, x, m, g, c):
return x[1]
ground.terminal = True
ground.direction = -1Solution
We integrate the system:
sol = integrate.solve_ivp(
model, [0., 10.], [0., 0.50, 50., 10.],
events=(apex, ground), args=(0.25, 9.81, 1.),
dense_output=True
)We refine the time grid based on the solution found:
t = np.linspace(sol.t.min(), sol.t.max(), 200)
x = sol.sol(t)We plot the refined solution and event coordinates:
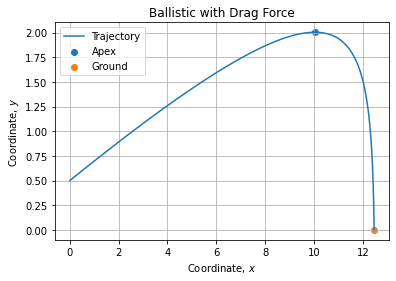
fig, axe = plt.subplots()
axe.plot(x[0,:], x[1,:], label="Trajectory")
axe.scatter(sol.y_events[0][0, 0], sol.y_events[0][0, 1], label="Apex")
axe.scatter(sol.y_events[1][0, 0], sol.y_events[1][0, 1], label="Ground")
axe.set_title("Ballistic with Drag Force")
# ...
It renders as follow: