Compute Acid/Base Partition functions

This post shows how to derive Acid/Base Partition functions using analytical chemistry and conversely how to determine pH of a mixture of poly-acid with given initial concentrations and pKa.

Partition functions

Partition functions are function expressing the percentage of a Acid/Base species with respect of pH. Lets take a simple example with a biprotic acid . If we express the sum of all species we have:

   

By isolating a species we can rewrite as follow:

   

Then using dissociation constants, we can write an expression only dependent of constants and :

   

Where is the partition function of substance . This equation can be rewritten as follow:

   

And indeed the sum of all partition function always equals to unity:

   

This procedure works for any number of protons, development strategy is the same.

Lets implement this in Python:

def cast_variables(pH, pKa):
    """
    Ensure pH and pKa have correct types and shapes
    """
    
    if not isinstance(pH, Iterable):
        pH = [pH]
    
    pH = np.array(pH)
    pKa = np.array(pKa)
    
    return pH, pKa

def alpha(i, pH, pKa):
    """
    Compute i-th partition function
    """
    
    pH, pKa = cast_variables(pH, pKa)
    
    n = len(pKa)
    H = np.power(10., -pH)
    Ka = np.power(10., -pKa)
    
    exponents = np.arange(i, -n + i - 1, -1)
    H_term = np.power(np.array([H]*(n + 1)).T, exponents)
    
    K_term = np.ones(exponents.size)
    for j in range(0, i):
        K_term[j] =  1. / np.prod(Ka[j:i])
    for j in range(i + 1, n + 1):
        K_term[j] =  np.prod(Ka[i:j])
        
    return 1. / np.sum(H_term * K_term, axis=1)

def alphas(pH, pKa):
    """
    Compute all partition functions
    """
    
    pH, pKa = cast_variables(pH, pKa)
    
    n = pKa.size + 1
    a = np.full((pH.size, n), np.nan)
    
    for i in range(n):
        a[:, i] = alpha(i, pH, pKa)
    
    if not np.allclose(np.sum(a, axis=1), 1.):
        raise ValueError("Partition functions does not sum up to unity")
    
    return a

With this code we can determine any composition of a mix of substance given their and the of the solution, for instance:

pKa = [2.148, 7.198, 12.319]
As = alphas(3.5, pKa)
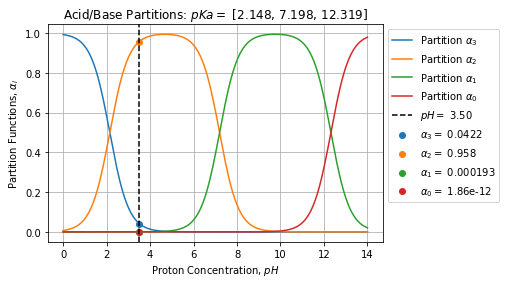
# array([[4.25621491e-02, 9.57245974e-01, 1.91877278e-04, 2.91087495e-13]])

This example is based on Phosphoric acid, we can see that at the major specie is which represent at most 95% of the mixture. The figure below shows the result reported over the partition curves:

pH of a mixture

Partition function are great if we know the pH and want to deduce the distribution of the species, but what if we would like to do the opposite: finding the pH for a given mixture of species? Well instead of drawing curves coming from math we will have to solve a non linear system.

For a -protic acid there are species governed by partition constants . We also need to determine the proton concentration in order to deduce the pH. That’s unknown with equations of the form:

   

At this point the system is undetermined for, but we can also write down the mass and charge balances which will provide equations and eventually make the system solvable.

The mass balance take into account the fact that the total concentration of species must be a predetermined constant :

   

The charge balance states the mixture is electrically neutral:

   

Where is also a predetermined constant in this problem.

Lets write the system and the solver for this problem in Python:

def system(C, pKa, Ct, Na):
    """
    System of equation to solve the pH of the mixture.
    Concentration C is n + 2 vector structured as follow: (H_nA, ..., A^n-, H^+)
    Ct is a constant for total concentration of species H_nA, ..., A^n-
    Na is a constant for total concentration of counter ion of ionised species H_n-1A^-, ..., A^n-
    
    There are n equilibria constants of the form:
    
    Ka_n = [H_n-1A^-] * [H^+] / [H_nA] 
    
    Mass balance:
    
    Ct = [H_nA] +  ... + [A^n-]
    
    Charge balance:
    
    [Na^+] = 0 * [H_nA] +  ... + n * [A^n-]

    Which provides n + 2 equations to solve n + 2 concentrations.
    """
    
    pKa = np.array(pKa)
    Ka = np.power(10., -pKa)
    
    return np.array([
        # Acid/Base Equilibria:
        (C[i + 1] * C[-1]) - C[i] * Ka[i]   
        for i in range(len(Ka))
    ] + [
        # Charge Balance:
        np.sum(np.arange(len(Ka) + 1) * C[:-1]) - Na,
        # Mass Balance:
        np.sum(C[:-1]) - Ct
    ])

def solve(C0, pKa, pH0=7.):
    """
    Solve the system for the given initial concentrations (including initial pH) and pKa.
    """
    
    H0 = np.power(10., -float(pH0))
    C0 = np.array(list(C0) + [H0])
    
    Ct = np.sum(C0[:-1])
    Na = np.sum(np.arange(C0[:-1].size) * C0[:-1])
    
    sol, info, code, message = optimize.fsolve(
        system, x0=[1.] * len(C0),
        args=(pKa, Ct, Na),
        full_output=True
    )
    
    if code != 1:
        raise ValueError("Solution not found: %s" % message)
    
    return {
        "C": sol[:-1],
        "alpha": sol[:-1] / Ct,
        "H": sol[-1],
        "pH": -np.log10(sol[-1]),
        "message": message,
    }

If we take our Phosphoric acid example, we can solve the pH a given mixture:

pKa = [2.148, 7.198, 12.319]
C0 = [0.5, 0.1, 0.1, 0.1]
sol = solve(C0, pKa)
#{'C': array([1.97682074e-01, 6.02301571e-01, 1.63553815e-05, 6.62477677e-13]),
# 'alpha': array([2.47102592e-01, 7.52876964e-01, 2.04442269e-05, 8.28097096e-13]),
# 'H': 0.0023342818425217543,
# 'pH': 2.6318467081611785,
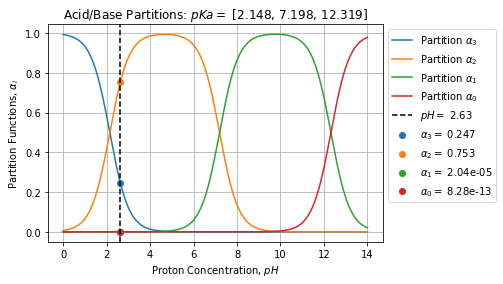
# 'message': 'The solution converged.'}

We deduce the pH of the mixture is about we can visualize the repartitions of the species on the figure below:

We can perform the same exercise with EDTA:

pKa = np.array([2.0, 2.7, 6.16, 10.26])
C0 = np.array([0.5, 0.3, 0.1, 0.1, 0.1])
sol = solve(C0, pKa)
# {'C': array([2.10454974e-01, 5.75492499e-01, 3.13993125e-01, 5.94019363e-05,
#         1.79493621e-12]),
#  'alpha': array([1.91322704e-01, 5.23174999e-01, 2.85448295e-01, 5.40017602e-05,
#        1.63176019e-12]),
#  'H': 0.0036569542594264933,
#  'pH': 2.436880471710877,
#  'message': 'The solution converged.'}

And graphically:

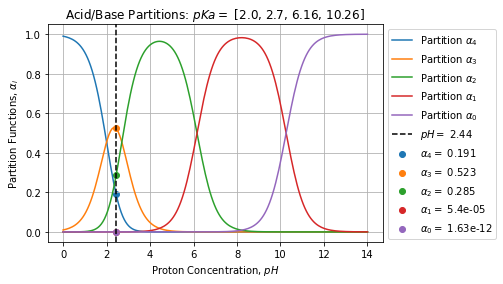
That is, with a bit a math and scipy solver fsolve we can simply determine composition and pH a solution of poly-protic acid.

Conclusions

We have computed partition of mixture in two different ways, allowing to cross check our computations. The major interest here is the pH solver which allows to predict the pH of a mixture of species when we know the initial concentrations added. On the other hand the partitions curves are helpful when choosing the composition of a buffer for example.

Bonus

As a bonus, the function to plot the curves and the solution if computed:

def plot(pKa, sol=None):
    """
    Plot partition curves and aditionnaly a solution if provided
    """
    n = len(pKa)
    pH = np.linspace(0, 14, 200)
    As = alphas(pH, pKa)
    labels = [r"Partition 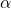" % i for i in reversed(range(n + 1))]
    
    fig, axe = plt.subplots()
    axe.plot(pH, As)
    
    if sol:
        axe.axvline(sol["pH"], linestyle="--", color="black")
        #axe.scatter([sol["pH"]] * len(sol["alpha"]), sol["alpha"], color="black")
        sols = []
        for i, a in enumerate(sol["alpha"]):
            axe.scatter([sol["pH"]], [a])
            sols.append(r"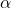 %.3g" % ((n-i), a))
        labels += ["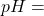 %.2f" % sol["pH"]] + sols
    
    axe.set_title("Acid/Base Partitions: 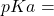 %s" % pKa)
    axe.set_xlabel(r"Proton Concentration, ")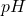
    axe.set_ylabel(r"Partition Functions, ")
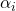    axe.legend(labels, bbox_to_anchor=(1, 1))
    axe.grid()
    
    return axe