This post details how principal component analysis (PCA) works and how to perform it step by step using Python.
Mathematics behind PCA
First we state the mathematical basis of PCA in order to get the full picture before applying it to real data.
Data decomposition
Consider the real matrix ![]() of
of ![]() observations of
observations of ![]() dimension, it’s always possible to decompose it into it’s Singular Value Decomposition ‐ which is a generalization of eigendecomposition ‐ as follow:
dimension, it’s always possible to decompose it into it’s Singular Value Decomposition ‐ which is a generalization of eigendecomposition ‐ as follow:
![]()
Or in its reduced form:
![]()
Where:
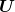 are principal components normalized to unit norm (
are principal components normalized to unit norm (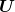 is a unitary matrix);
is a unitary matrix);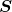 are singular values (
are singular values (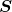 is a diagonal matrix);
is a diagonal matrix);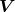 are singular vectors (
are singular vectors (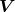 is an orthogonal matrix, and
is an orthogonal matrix, and 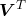 is an orthonormal basis of principal components space).
is an orthonormal basis of principal components space).
Covariance decomposition
Consider the covariance matrix ![]() defined as follow:
defined as follow:
![]()
Where ![]() is necessarily centered to origin (mean of each column is zero).
is necessarily centered to origin (mean of each column is zero).
Using the SVD decomposition defined above, the covariance matrix can be expressed as:
![]()
Which proves the covariance matrix is eigen-decomposable and has the same orthonormal basis than the SVD of the data matrix ![]() . The relation between singular values
. The relation between singular values ![]() and the eigen values
and the eigen values ![]() is then defined as
is then defined as ![]() .
.
Also, notice:
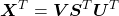 by transposition;
by transposition;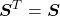 because
because 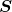 is diagonal;
is diagonal;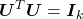 because
because 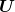 is unitary;
is unitary;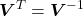 because
because 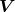 is orthogonal.
is orthogonal.
Variance conservation
A nice property of PCA is it conserves the total variance of the dataset. Covariance matrix is real symmetric and therefore by the spectral theorem it is diagonalizable.
![Rendered by QuickLaTeX.com \[\mathrm{Tr}\left[\mathrm{Cov}(\boldsymbol{X})\right] = \mathrm{Tr}\left[\boldsymbol{V}\boldsymbol{E}\boldsymbol{V}^{-1}\right] = \mathrm{Tr}\left[\boldsymbol{E}\boldsymbol{V}\boldsymbol{V}^{-1}\right] = \mathrm{Tr}\left[\boldsymbol{E}\right] = \sum\limits_{i=1}^{k} \lambda_i\]](https://landercy.be/wp-content/ql-cache/quicklatex.com-e6c4e33e476cebd40f5b2ef4c787f989_l3.png)
Notice than trace for matrix commutation are equals ![]() .
.
Which proves that the total variance of the dataset is conserved and is equal to the sum of eigenvalues.
Principal components
Principal components ![]() are the projection of observations in
are the projection of observations in ![]() into the principal components space defined by the columns of
into the principal components space defined by the columns of ![]() . Performing the change of basis leads to:
. Performing the change of basis leads to:
![]()
Principal components ![]() are the unitary principal components
are the unitary principal components ![]() scaled by singular values
scaled by singular values ![]() by decreasing order of magnitude.
by decreasing order of magnitude.
This is where PCA becomes useful. Because it allows to capture a maximum of variance in the very first dimensions of its principal components. Therefore dimensionality of dataset can be reduced while keeping a maximum of information. This can be assimilated to a compression.
PCA Loadings
Lets define standardized principal components ![]() as follow:
as follow:
![]()
Loadings ![]() can be defined as the covariance between data matrix
can be defined as the covariance between data matrix ![]() and standardized principal components
and standardized principal components ![]() :
:
![]()
Warning: definition of loadings are not universal and generally depends on software implementation. For instance, the definition above has been chosen for its clean mathematical point of view. Although it is a common definition, there are software (such as R) which compute loadings in a different way.
PCA, step by step
First, lets import some modules and a dataset to shoulder our computations:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import linalg
data = sns.load_dataset("iris")
target = data.pop("species")
X = data.valuesDetailed computations and sanity checks
We center the dataset (required):
n, k = X.shape # (150, 4)
Xm = X.mean(axis=0) # [5.84333333, 3.05733333, 3.758 , 1.19933333]
X -= XmWe also compute the standard deviation and the total variance:
Xs = X.std(axis=0, ddof=1) # [0.82806613, 0.43586628, 1.76529823, 0.76223767]
Vx = np.sum(Xs ** 2) # 4.572957046979866From X we can compute the Covariance matrix and check it is symmetric and positive definite:
C = X.T @ X / (n - 1)
np.allclose(C, C.T) # True
np.all(linalg.eigvals(C) > 0) # True
linalg.cholesky(C) # ExistsNow we can perform the SVD and confirm the decomposition is correct:
U, s, Vt = linalg.svd(X, full_matrices=False)
S = np.diag(s)
V = Vt.T
np.allclose(X, U @ S @ Vt) # TrueWe can also confirm matrices are unitary/orthogonal:
np.allclose(np.eye(k), U.T @ U) # True
np.allclose(np.eye(k), V.T @ V) # True
np.allclose(V.T, linalg.inv(V)) # TrueAlso notice than matrix U is centered to origin and normalized by columns:
np.mean(U, axis=0) # [0., 0., 0., 0.]
linalg.norm(U, axis=0) # [1., 1., 1., 1.]We confirm variance is conserved (redistributed among eigenvalues):
E = S ** 2 / (n - 1)
np.allclose(Vx, np.sum(E)) # TrueNow we can perform the projection into the principal components space:
Z = X @ V
np.allclose(Z, U @ S) # TrueAnd finally we can compute loadings:
Y = np.sqrt(n - 1) * U
L = V @ S / np.sqrt(n - 1)
np.allclose(L, X.T @ Y / (n - 1)) # TrueSummary
Now we can summarize the whole operation into these few lines:
U, s, Vt = linalg.svd(X, full_matrices=False)
S = np.diag(s)
V = Vt.T
E = S ** 2 / (n - 1)
Z = U @ S
L = V @ S / np.sqrt(n - 1)The same goal can be achieved with sklearn:
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(X)
V = pca.components_.T
E = np.diag(pca.explained_variance_)
L = V @ np.sqrt(E)Visualizations
Two figures are generally associated with PCA: Variance Plot and Bi Plot.
The first figure shows how the variance is distributed among the principal components and is used to help to find the right amount of dimension to keep.
c = np.arange(k)
rVx = np.diag(E) / Vx
SrVx = np.cumsum(rVx)
from matplotlib.ticker import MaxNLocator
fig, axe = plt.subplots()
axe.bar(c, rVx, alpha=0.7)
axe.plot(c, SrVx, "-o")
for i in c:
axe.text(c[i], SrVx[i], "%.3f" % SrVx[i])
axe.set_title("PCA: Variance Explained")
axe.set_xlabel("Principal Components Index")
axe.set_ylabel("Variance explained")
axe.xaxis.set_major_locator(MaxNLocator(integer=True))
axe.grid()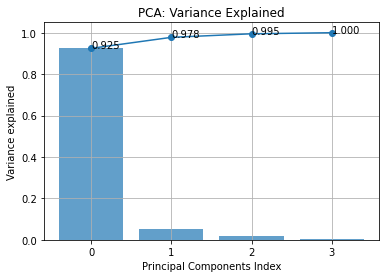
In this example, we see that if we keep the two first component we capture at least 97.8% of the variance, which is totally acceptable.
The second figure shows the data projected into the reduced principal components space and how each variable contributes to each component (loadings):
fig, axe = plt.subplots()
for key in target.unique():
q = target == key
axe.scatter(*Z[q, :2].T, label=key)
for i in range(k):
axe.arrow(0, 0, *L[i, :2])
axe.text(*L[i, :2], str(i))
axe.set_title("PCA: Bi Plot")
axe.set_xlabel("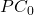 ")
axe.set_ylabel("
")
axe.set_ylabel("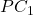 ")
axe.legend()
axe.grid()
")
axe.legend()
axe.grid()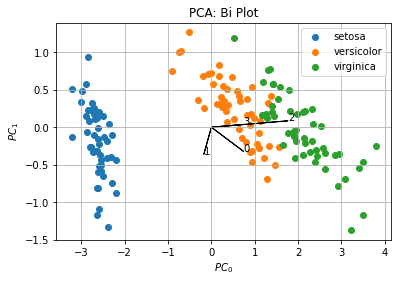
In this example, we see the two first components and loadings according to our definition. This figure allows us to see clusters in the dataset by taking the best snapshot of it (projection with more explained variance).
Loadings inform us than the first variable contributes to both components, while second variable contributes more to the second component, finally third and fourth variables mainly contribute to the first principal component.
