Equation of locus of maximum rates for an exothermic reversible reaction

This post explains how to drawn the exact equation of the locus of maximum rates for an exothermic reversible reaction.

Model

We define the simple following reaction:

    \[A \underset{k_{inv}}{\overset{k}{\rightleftharpoons}} B\]

With rate v is defined as:

    \[v = k A - k_{inv}B\]

Where the thermodynamic and kinetic constants K(T) and k(T) are modeled as:

    \[K(T) = K_0 \exp\left( - \frac{\Delta_RH^0}{RT} \right) \,,\quad k(T) = k_0 \exp\left( - \frac{E_a}{RT} \right)\]

Defining the conversion ratio x, concentrations can be expressed as A = A_0(1 - x), B = A_0 x assuming there is no product B at the beginning. Then we can state:

    \[K(T) = \frac{B}{A} = \frac{x_e(T)}{1 - x_e(T)} \Leftrightarrow x_e(T) = \frac{K(T)}{1 + K(T)}\]

Where x_e(T) is the equilibrium conversion ratio for a given temperature T. This equation is the envelope of all other curves as it is impossible to go beyond the equilibrium.

Similarly, reaction rate can be written in term of x:

    \[v = k(T) A_0 (1-x) - \frac{k(T)}{K(T)} A_0 x = A_0 k(T) \left[ 1 - \frac{x}{x_e(T)} \right]\]

And isolate x for a given rate v:

    \[x(T, v) = x_e(T) \left[ 1 - \frac{v}{A_0 k(T)} \right]\]

For an exothermic equilibrium those curves are concave (negative convexity) and therefore exhibits maximum. Putting \frac{\partial}{\partial T}x(T,v) = 0 and solving for x, we get the following expression:

    \[x_{otp}(T) = \frac{E_a K(T)}{E_a - \Delta_RH^0 + E_a K(T)}\]

Which is the locus of maximum rates (optimal temperature pathway) for the given reaction.

Symbolic check

We can check out the math using sympy:

import sympy as sp

R = sp.Symbol("R", positive=True)
T = sp.Symbol("T", positive=True)
DrH = sp.Symbol("\Delta_{R}H^0")
x = sp.Symbol("x", postive=True)
xe = sp.Symbol("x_e")
K0 = sp.Symbol("K_0")
Ea = sp.Symbol("E_a")
k0 = sp.Symbol("k_0")
A0 = sp.Symbol("A_0")
v = sp.Symbol("v")

KT = K0 * sp.exp(- DrH / (R * T))
xe = KT / (1 + KT)
kT = k0 * sp.exp(- Ea / (R * T))
vT = A0 * kT * (1 - x / xe)
xTv = xe * (1 - v / (A0 * kT))

sol = sp.solve(sp.Eq(sp.diff(xTv, T), 0), v)
sol2 = sp.solve(sp.Eq(sol[0], vT), x)
# [E_a*K_0/(E_a*K_0 + E_a*exp(\Delta_{R}H^0/(R*T)) - \Delta_{R}H^0*exp(\Delta_{R}H^0/(R*T)))]

Which is same expression that we derived above.

Numerical example

Lets write a small class that brings the math:

import numpy as np
import matplotlib.pyplot as plt

class Equilibrium:
    
    R = 8.314
    
    def __init__(self, DrH0, K0, Ea, k0, A0=1.):
        self.DrH0 = DrH0
        self.K0 = K0
        self.Ea = Ea
        self.k0 = k0
        self.A0 = A0
        
    def K(self, T):
        return self.K0 * np.exp(- self.DrH0 / (self.R * T))
    
    def xe(self, T):
        return self.K(T) / (1. + self.K(T))
    
    def k(self, T):
        return self.k0 * np.exp(- self.Ea / (self.R * T))
    
    def v(self, T, x):
        return self.A0 * self.k(T) * (1. - x / self.xe(T))
    
    def x_otp(self, T):
        return self.Ea * self.K(T) / (self.Ea - self.DrH0 + self.Ea * self.K(T))

And create a real world example:

model = Equilibrium(-75300, 0.18955e-10, 48721, 530991)

Tlin = np.linspace(250, 500, 500)

vlevels = np.logspace(-6, -1, 15)
xlin = np.linspace(0., 1., 500)
T, X = np.meshgrid(Tlin, xlin)
xisov = model.v(T, X)

fig, axe = plt.subplots()
c = axe.contour(T, X, xisov, vlevels)
axe.plot(Tlin, model.xe(Tlin), linewidth=2.)
axe.plot(Tlin, model.x_otp(Tlin))

Which renders as follow:

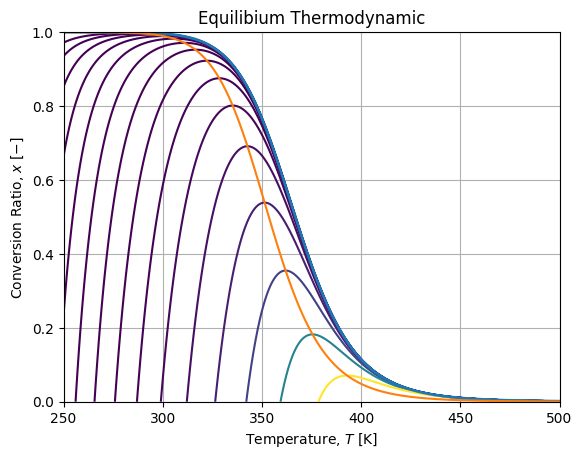
Where the blue curve is the equilibrium envelope, the orange curve is the locus of maximum rates.

Tags
jlandercy
jlandercy
Articles: 27

Related Posts

Leave a Reply